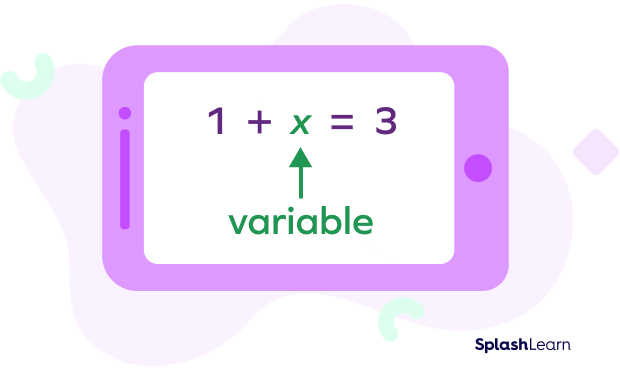
Algebra is the part of mathematics that helps represent problems or situations in the form of mathematical expressions. In algebra, we use numbers like 2, −7, 0.068 etc., which have a definite or fixed value. In algebra we use variables like x, y, and z along with numbers.
Signs used in algebra
Mathematical operations like multiplication (×), division (÷), addition (+), and subtraction (−) are used to form a meaningful mathematical expression.
There are other signs and symbols that are also frequently used in algebra.
equal to (=), not equal to (≠), less than (<), greater than (>), less than equal to(≤), greater than equal to ( ≥).
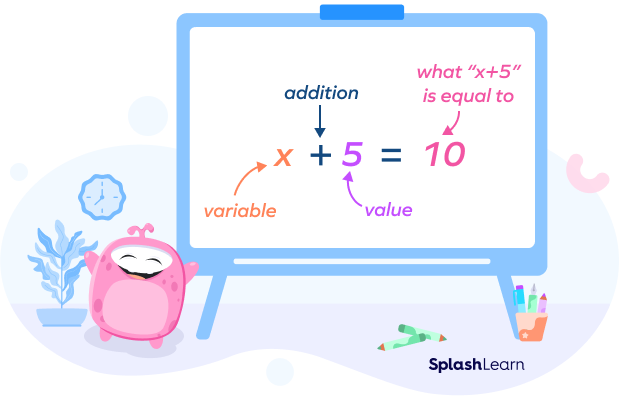
A straightforward example of an equation in algebra is x + 5 = 10.
Algebra A Puzzle
Algebra is all about puzzles.
Here is one for you.
⬜+ 10 = 13
⬜ plus 10 is equal to 13.
We have to find the number in this box, and what number, when added to 10, gives us 13. Simple, it’s three; we can see that 3 plus 10 equals 13. The puzzle we see here contains only numbers.
We can also say that x plus 10 equals 13. Find x.
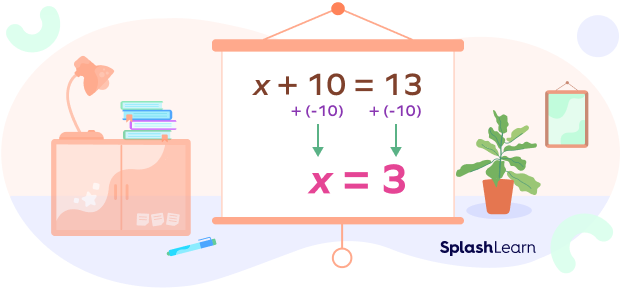
We use the letter in place of the box. These letters are also called variables, sometimes referred to as the unknown since their values are unknown to us.
 Begin here
Begin here
Writing the Statements in Algebraic Form.
- The total cost of 1 kg apple and 2 kg of guava is $3. If x represents the cost of 1 kg apple and y represents the cost of 1 kg guava, then this statement is represented in the form of an algebraic expression as:
x + 2y = 3
- If the area of the rectangle is 36 cm2. Its length is represented as l and width is represented as b. Then this statement is represented as :
l × b = 36
Solved Examples on Algebra
Question 1: William had a few chocolates with him. Jack came across and took away five of his chocolates. And then he had just seven chocolates remaining with him. How many chocolates did he have before Jack came to him?
Answer: Assume William had x chocolates with him, and Jack took away five of his chocolates.
x − 5 = 7
So, we subtract five from x. Moreover, after all this, William was left with seven chocolates. This entire puzzle will then equal seven.
x − 5 + 5 = 7 + 5
x = 12
Question 2: A magician was invited to perform at a birthday party. The magician arrived at the party with 18 balloons. On the way, 7 balloons got blown away. So how many balloons did the magician have in the beginning?
Answer: We can solve this problem using algebra, x − 7 = 18.
So, we subtract seven from x, and after that, we are left with 18 balloons.
Now, all we have to do is find x.
x − 7 + 7= 18 + 7
x = 18 + 7
x = 25
Question 3: Amman wants to visit a zoo. A ticket for the entry to the zoo cost $4. He has only $3. How much more money does he need to buy the ticket?
Answer: Let Amman need $y more to buy the ticket.
So, we will solve this problem using algebra, 3 + y = 4
We add y to 3 to get 4.
Now we need to find the value of y.
3 + y − 3 = 4 − 3
y = 4 − 3
y = 1
Practice Problems on Algebra
Algebra
Write this statement as an equation: 4 times a number equals 40.
Times here means multiplication (×).
A number is not specified so we take a variable y and write the equation 4 × y = 40.
There were 90 kites in a shop, and the shopkeeper was left with only 5 kites. How many kites does the shopkeeper sell?
Let the shopkeeper sell x kites.
90 − x = 5
So x = 85
Evaluate the expression 4t + 7 for t = 2.
4t + 7 = 4(2) + 7 = 8 + 7 = 15
There are only 5 books on the study table, but you have 14 books. How many books are missing from the study table?
Let x books be missing from the study table.
14 − x = 5
So, x = 9
Frequently Asked Questions on Algebra
Six less than a number equals two. What is the number?
Let us assume the number to be a variable. Let the number be x. As per the question, we can write x – 6 = 2. On solving this, we get x = 8. Therefore, the required number is 8.
What are the different types of Algebraic Expressions?
Different types of algebraic expression include: Monomial (Example :7f), Binomial (Example: 4l + 3m), Trinomial (Example: 3x + 5y + 6z), Quadratic (Example: 5x2 + 2x − 9 ) cubic (Example: 2x3 − 4x2 + 3x −4 ).
What are the four rules of algebra?
Commutative Rule of Addition, Commutative Rule of Multiplication, Associative Rule of Addition, Associative Rule of Multiplication, Distributive Rule of Multiplication.
What are the basic terms of Algebra?
Basic terms in algebra are numbers, constants, equations, variables, linear equations, quadratic equations, etc.




