Fractions are often referred to as numbers between numbers. Fractions are numerical values that represent a part or a portion of a whole. For example, look at the pizza below.

This pizza has been cut into 4 equal parts. So each piece of the pizza represents 1 out of 4 equal parts. So mathematically, we can represent each piece as $\frac{1}{4}$. This number is called a fraction.
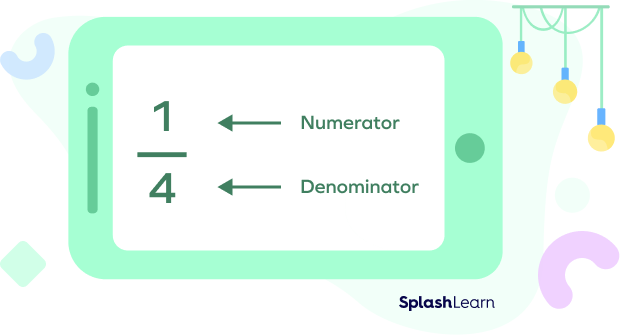
The number below the bar that represents the total number of equal parts that the whole is divided into is called the denominator.
And the number on the top that represents the number of equal parts we are considering is called the numerator.
What is an Improper Fraction?
Before discussing improper fraction, we first need to understand proper fractions.
Proper fractions: Fractions for which the numerator is less than the denominator are called proper fractions. For example, if you order a pizza and cut it into 4 equal parts, and then eat one slice out of it, the remaining pizza can be expressed as $\frac{3}{4}$ of the whole pizza. Here, since 3 is less than 4, the fraction is a proper fraction.

Improper fractions: Improper fractions are defined as fractions for which the numerator is greater than the denominator. Let us take an example of improper fraction, imagine you order a pizza that has 4 slices. Your friends eat all 4 slices. And you realize you didn’t get any. You order another pizza. After eating 1 slice from it, you realize you are done eating. So, how much of the pizza did your friends and you have in all?
Your friends first had all 4 slices of 1 pizza, and then you had 1 slice of the same size from the second pizza.
So, the total pizza eaten is $\frac{5}{4}$ slices of pizza. And that’s an improper fraction with a numerator greater than the denominator.

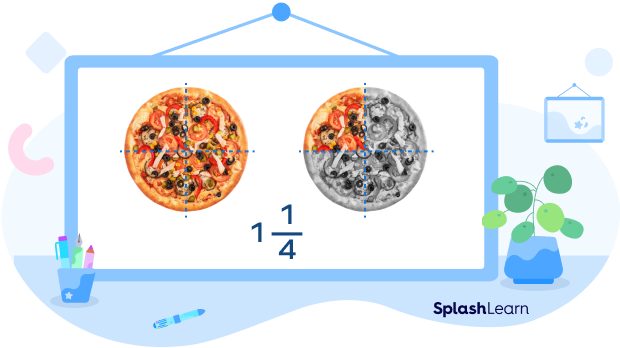
Mixed numbers: Mixed numbers are just another way of writing fractions greater than a whole. A mixed number has a whole part and a fractional part, which is actually a proper fraction.
Let’s take the same example from above. You and your friends ate one whole pizza and one-fourth of a pizza. As a mixed fraction, we can write this as $1$ and $\frac{1}{4}$ of a pizza or $1\frac{1}{4}$ of a pizza.
 Begin here
Begin here
Fraction Conversion
Improper Fraction to Mixed Number
An improper fraction can be converted to a mixed fraction and a mixed fraction can be converted to an improper fraction.
Let’s say we want to convert the fraction $\frac{7}{2}$ into a mixed number.
Step 1: Find the quotient and the remainder by dividing the numerator with the denominator.
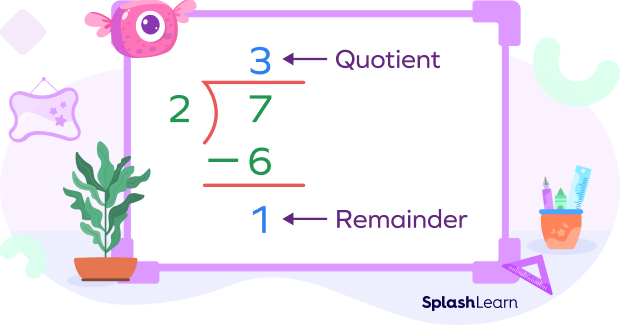
Step 2: The quotient will be the number of wholes for the mixed number. The remainder will be the numerator of the fractional part and the denominator will remain the same.
So, the mixed number form of $\frac{7}{2}$will be:

Mixed Number to Improper Fraction
Any mixed number can be converted into an improper fraction.
Let’s say we want to convert the mixed number $1\frac{3}{4}$ into an improper fraction.
Step 1: Multiply the denominator with the whole. And then add the numerator to the product.

Step 2: Keep the denominator same and solve for the numerator.

Therefore, the improper fraction for the mixed number $1\frac{3}{4}$ will be $\frac{7}{4}$.
Related Worksheets
Solved Examples on Improper Fractions
Example 1. Identify the improper fractions:
$\frac{1}{5}$, $2\frac{7}{5}$, $\frac{3}{2}$, $\frac{1}{3}$, $\frac{5}{4}$, $6 \frac{1}{6}$
Solution: $\frac{2}{3}$ and $\frac{5}{4}$ are improper fractions as the value of the numerator is greater than the value of the denominator for both of these fractions.
Example 2. Write $4\frac{2}{7}$ as an improper fraction.
Solution: Converting $4\frac{2}{7}$ into an improper fraction,
$4 \frac{2}{7}$ = $\frac{(7\times4) + 2}{7}$ = $\frac{30}{7}$
Example 3. Write $2\frac{9}{6}$ as an improper fraction.
Solution: While dividing 29 by 6, the quotient and remainder are 4 and 5 respectively.
So $\frac{29}{6}$ written as a mixed number is $ 4 \frac{5}{6}$ .
Converting $3\frac{1}{5}$ to an improper fraction:
Practice Problems on Improper Fractions
What are Improper Fractions? Meaning, Definition, Examples
What type of fraction is $\frac{11}{4}$?
Since the value of the numerator is greater than the denominator, the given fraction is an improper fraction.
Write the mixed number $3\frac{1}{5}$ as an improper fraction.
Converting $3\frac{1}{5}$ to an improper fraction:
$3\frac{1}{5}$ = $\frac{(5\times 3) + 1}{5}$ = $1\frac{6}{5}$
Identify the improper fraction.
The value of the numerator is greater than the value of the denominator in $\frac{12}{11}$. Therefore, it is an improper fraction.
Convert $\frac{5}{2}$ into a mixed fraction.
Dividing 5 by 2, we get the quotient and the remainder as 2 and 1 respectively.
The quotient becomes the whole number, the remainder becomes the numerator of the fractional part and the denominator remains the same.
Frequently Asked Questions on Improper Fractions
Which are easier for calculations: improper fractions or mixed fractions?
Improper fractions are easy for arithmetic operations of addition, subtraction, multiplication, and division. Mixed fractions are easier to understand and represent in figures.
Why are fractions important?
Every quantity cannot be expressed in whole numbers. Fractions are employed to indicate a certain part or portion of any item. They are a fundamental concept in computation and applied in algebra, ratios, and several other concepts in mathematics and other fields.
How are decimals related to fractions?
Fractions and decimals are both ways to represent quantities or numbers. Decimals are nothing but a different way to represent fractions whose denominator is 10 or powers of 10. For example, the fraction $\frac{15}{10}$ in decimal form is 1.5.





















