Subtracting Mixed Numbers – Definition with Examples

Subtracting Mixed Numbers

Fractions which are more than a whole are known as mixed fractions or mixed numbers.

For instance: Nicholas has 3 chocolates, and each chocolate has 3 bars. He eats 7 bars of chocolate, which means 2 whole chocolates and 1 bar of the third chocolate.

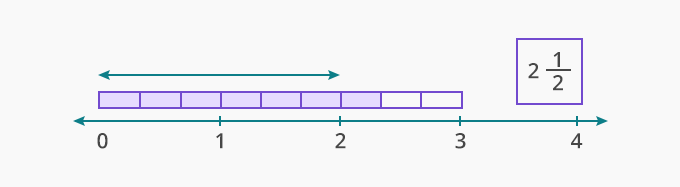
Real-life examples of Subtracting mixed numbers:

Begin here

Make 10 Strategy

Add 1-Digit Numbers Game

Play

Add 2-digit number to 1-digit

Add 2-Digit and 1-Digit Numbers Game

Play

Regroup and add 2-digit numbers

Add 2-Digit Numbers By Regrouping Game

Play

Add Three Whole Numbers

Add 3 Numbers Game

Play

Add Three Whole Numbers

Add 3 Numbers in Any Order Game

Play

Introduction to Addition

Add 3 Numbers Using Groups of Objects Game

Play

Add Three Whole Numbers

Add 3 Numbers using Model Game

Play

Add within 1000 without Regrouping

Add 3-Digit and 1-Digit Numbers and Match Game

Play

Add 3-digit number to 1-digit

Add 3-Digit and 1-Digit Numbers Game

Play

Add within 1000 with Regrouping

Add 3-Digit and 1-Digit Numbers with Regrouping Game

Play

How to Subtracting mixed numbers?

Case 1: Subtracting mixed numbers with same denominators

Follow the given steps to subtract mixed numbers with same denominators:

Step 1– Subtract the wholes.                 

Step 2– Convert the fractions into improper fractions.

Step 3– Subtract the fraction.

Step 4– Change the improper fraction into a mixed number if needed.

Step 5– Write the mixed number with wholes and the fraction.

Example 1: 5 ⁷⁄₃ – 3 ²⁄₃

Step 1 – Subtract 3 from 5.

              5 – 3 =2

Step 2 – Subtract the fractions:

             ⁷⁄₃ – ²⁄₃

Step 3 – Write the fraction with whole.

              5 ⁷⁄₃ – 3 ²⁄₃ = 2 ⁵⁄₃ 

Case 2: Subtracting mixed numbers with different denominators

Follow the given steps to subtract mixed numbers with different denominators:

Step 1– Convert the mixed numbers into improper fractions.

Step 2– Find the common multiple of both the denominators.

Step 3– Convert the fractions as common denominators.

Step 4– Solve the fractions.

Step 5– Convert the fraction as a mixed number.

Example 2: 6 ¹⁄₂ – 1 ³⁄₄

Step 1– Convert the mixed numbers into improper fractions.

             1 ³⁄₂ – ⁷⁄₄

Step 2– Find the common multiple of both the denominators 2 and 4.

The common multiple of 2 and 4 is 4. 

Step 3– Convert the fractions as common denominators.

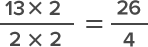
Step 4– Solve the fractions

               ²⁶⁄₄ – ⁷⁄₄ = ¹⁹⁄₄

Step 5– Convert the fraction as a mixed number.

                ¹⁹⁄₄ = 4 ³⁄₄