What is Obtuse Triangle?
An obtuse-angled triangle is a triangle in which one of the interior angles measures more than 90° degrees. In an obtuse triangle, if one angle measures more than 90°, then the sum of the remaining two angles is less than 90°.
For better understanding, look at the following example.
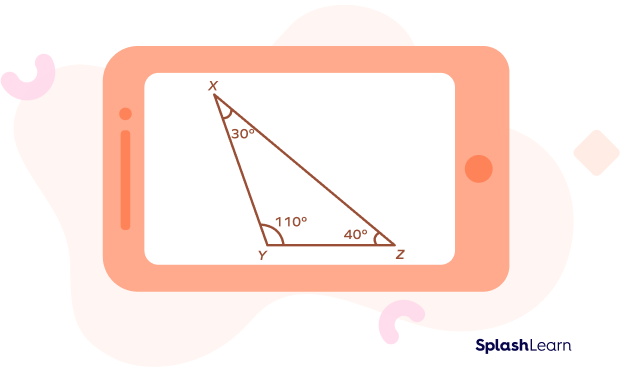
In this image, triangle XYZ has an obtuse angle at Y. Therefore, this triangle is an obtuse-angled triangle. Note that the other two angles are less than 90 degrees, and all the angles of the triangle add up to 180 degrees.
 Begin here
Begin here
Real-life Examples

A cloth-hanger has an obtuse angle where the hook is attached at the top.
Related Worksheets
Non-Examples of Obtuse Angles

In the above examples, we can clearly see that the triangle shapes do not have an angle greater than 90°. Therefore, this is not an obtuse triangle.
Special Facts About the Obtuse Triangle
- An equilateral triangle can never be obtuse. Since an equilateral triangle has equal sides and angles, each angle measures 60°, which is acute. Therefore, an equilateral angle can never be obtuse-angled.
- A triangle cannot be right-angled and obtuse-angled at the same time. Since a right-angled triangle has one right angle, the other two angles are acute. Therefore, an obtuse-angled triangle can never have a right angle and vice versa.
- The side opposite the obtuse angle in the triangle is the longest.
Types of an Obtuse Triangles
- Isosceles obtuse triangle: Here, two sides of the triangle have equal lengths.
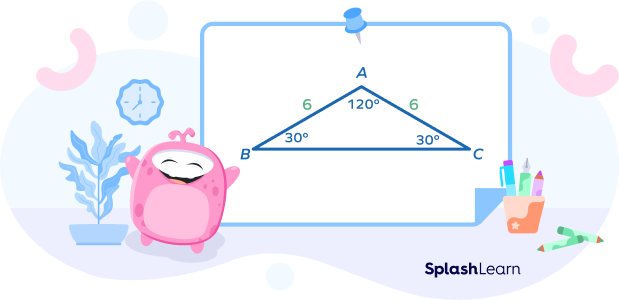
- Scalene obtuse triangle: All sides are unequal in this type of obtuse triangle.
Solved Examples on Obtuse Triangle
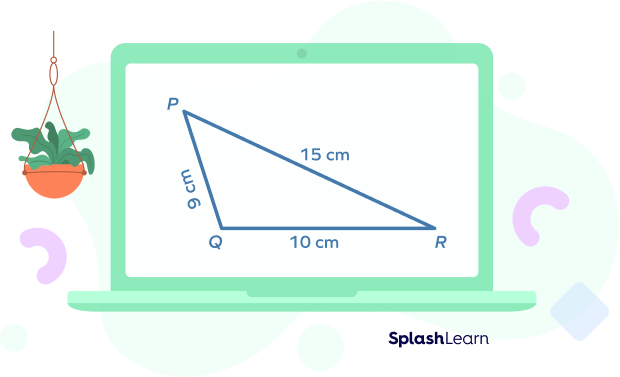
- Is the following picture an example of an obtuse triangle?
Answer:
No, the given figure is not an obtuse triangle as all the angles are less than 90°.
- Will the following set of angles form an obtuse triangle?
95°, 30°, 55°.
Answer: Yes, these angles will form an obtuse-angled triangle, as 95 degrees is an obtuse angle and the sum of the angles(95 + 30 + 55) is 180 degrees.
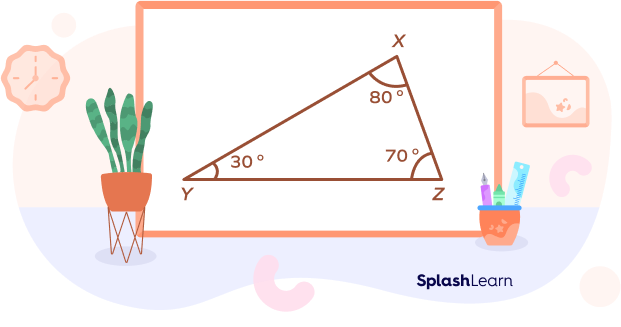
- What type of obtuse triangle is shown in the figure?
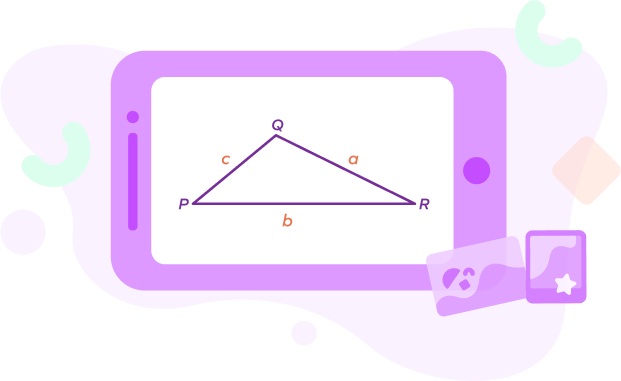
Answer: It is an obtuse scalene triangle as none of its sides are equal.
Practice Problems on Obtuse Triangle
Obtuse Triangles
Which of the following sets of angles form an obtuse triangle?
An obtuse triangle has one obtuse angle. The other two angles are acute angles.
A triangle has an angle of 110 degrees, and the other two angles are equal. What will be the measure of the other two angles?
The sum of the other two angles is 180° − 110° = 70°. Hence, the other two angles will measure 35° each.
An obtuse triangle has sides measuring 3 cm, 4 cm, and 6 cm. What is the perimeter of the triangle?
Perimeter of the obtuse triangle = 3 + 4 + 6 = 12 cm
Frequently Asked Questions on Obtuse Triangle
Can a triangle have two obtuse angles?
No, a triangle cannot have two obtuse angles, as the sum of the three angles cannot exceed 180 degrees.
How do you distinguish between acute and obtuse triangles?
Obtuse triangles have one angle that’s greater than 90°. In acute triangles, all the angles are less than 90°.
Can an obtuse triangle have one right angle?
No, a triangle cannot have both obtuse and right angles, as the sum of the three angles cannot exceed 180 degrees.
How do you know if a triangle is obtuse?
We can easily identify an obtuse triangle by looking at its angles. If any angle measures more than 90°, that triangle is an obtuse triangle.













