Area and Perimeter – Definition with Examples

Area and Perimeter

Perimeter for a 2-dimensional shape is the total distance around the respective shape. For the figures with straight sides such as triangle, rectangle, square or a polygon; the perimeter is the sum of lengths for all the sides.

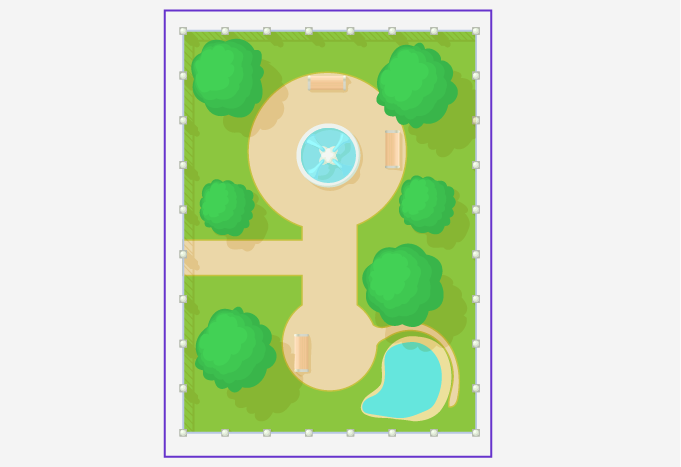
The peripheral border in blue is the perimeter of the park.

Area

The area for a 2-dimensional shape is the space enclosed within the perimeter of the given shape. To calculate the area for different shapes, use different formulas based on the number of sides and other characteristics such as angles between the sides.

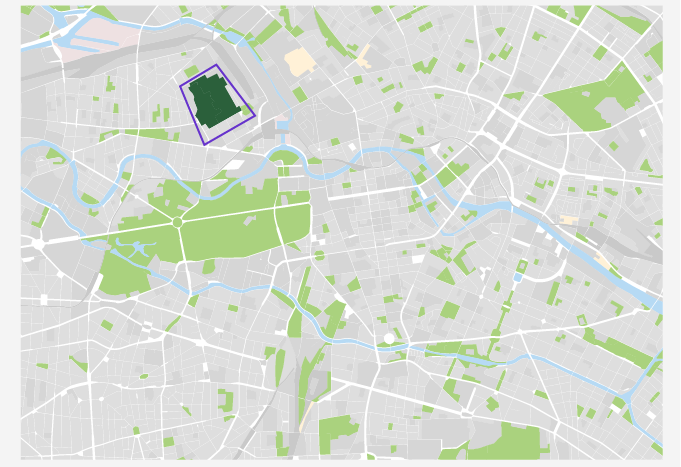
The area for the park is shown in dark green color.

Calculating Area and Perimeter for Different Shapes

Triangle

The formulas for calculating the perimeter and area of a triangle ABC are:

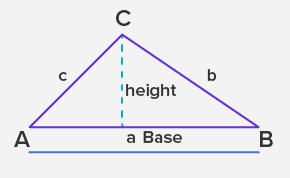
• Perimeter = a + b + c

                       ⇒ Perimeter = sum of the length of all sides

                       ⇒ Perimeter = a + b + c

• Area = ¹⁄₂ × base × height

Square

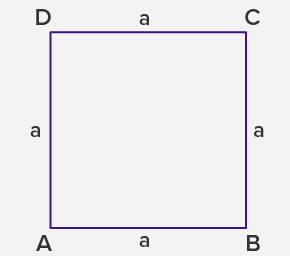
• Perimeter = 4a

                       ⇒ Perimeter = sum of lengths of all sides

                       ⇒ Perimeter = a + a + a + a

                       ⇒ Perimeter = 4a

• Area = a²

                ⇒ Area = length × breadth

                ⇒ area = a × a 

                ⇒ area = a²

Rectangle

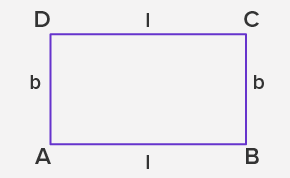
• Perimeter = 2 (l + b)

                       ⇒ Perimeter = sum of lengths of all sides

                       ⇒ Perimeter = l + b + l + b

                       ⇒ Perimeter = 2 × (l + b)

• Area = l × b

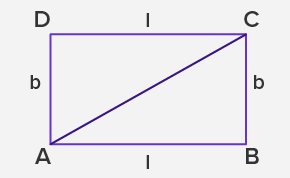
       ⇒ Area = Area (ABC) + Area (ADC)

       ⇒ Area = 2 × Area (ABC)

       ⇒ Area = 2 × (¹⁄₂ × base × height)

       ⇒ Area = base × height

       ⇒ Area = l × b

Units of Measurement

If all the measurements are in centimeter, the units of measurement for the perimeter and area of different shapes are:

• Perimeter = sum of sides

               Thus, the unit of measurement remains the same, as cm

• Area = product of sides

               The unit of measurement is unit2 or cm2

Application

The concepts of area and perimeter are the basis for understanding Euclidean geometry and calculating the volume of solid shapes in 3-dimensional space such as cones, prism, sphere, and cylinder. Also, we use these formulas for calculating the area and perimeter for quadrilaterals and polygons comprising of sides and curves. The real-life utility of the concept is in several fields such as mapping, architecture, and surveying. The geometric representation of figures is done by sketching the distances and areas for clear understanding.

Three-dimensional objects derived from 2-dimensional shapes and land surveying in fields.

Fun Facts

Practice Problems on Area and Perimeter

Area and Perimeter Attend this Quiz & Test your knowledge. 1 The area of a triangle with a base of 7 units is 21 square units. What is the height of the triangle? 2 units 3 units 4 units 6 units CorrectIncorrect Correct answer is: 6 units The area of a triangle is 1/2 ✕ base ✕ height. So, height of the triangle = (2 ✕ area)/base, i.e., (2 ✕ 21 square units)/7 units = 6 units. 2 What is the area of a triangle with a base of 6 units and a height of 10 units? 16 square units 30 square units 32 square units 60 square units CorrectIncorrect Correct answer is: 30 square units The area of a triangle is 1/2 ✕ base ✕ height, i.e., 1/2 ✕ 6 cm ✕ 10 cm or 30 square units. 3 If the area of a square is 36 square cm. What is its perimeter? 9 cm 12 cm 18 cm 24 cm CorrectIncorrect Correct answer is: 24 cm The area of a square is side ✕ side. Also, 36 = 6 ✕ 6. So, the side of the square = 6 cm. Thus, the perimeter of the square = 4 ✕ side, i.e., 4 ✕ 6 cm or 24 cm. 4 What is the perimeter of a regular pentagon of side 8 cm? 32 cm 40 cm 64 cm 80 cm CorrectIncorrect Correct answer is: 40 cm The perimeter of a regular pentagon is 5 ✕ side, i.e., 5 ✕ 8 cm or 40 cm.